Contents
What is dyscalculia
Dyscalculia is a type of learning disorder, that is defined as difficulty in learning to calculate or difficulty acquiring basic arithmetic skills that is not explained by low intelligence or inadequate schooling 1. Students with dyscalculia have difficulty understanding simple number concepts, lack an intuitive grasp of numbers, and have problems learning number facts and procedures. Dyslexia and dyscalculia can co-exist or they can exist independently of one another. About 5% and 15% of primary school children are affected 2. Dyscalculia does not improve without treatment 1. The early identification and treatment of dyscalculia are very important in view of its frequent association with mental disorders 3. Sufferers need a thorough, neuropsychologically oriented diagnostic evaluation that takes account of the complexity of dyscalculia and its multiple phenotypes and can thus provide a basis for the planning of effective treatment.
The areas of maths that students with dyslexia find most difficult are:
- The language of maths. Some students struggle to read and understand the vocabulary in maths questions, and therefore don’t know what task they are being asked to do. Many different words can be used to describe the same action, e.g. add, increase, plus, total.
- Sequencing. The learning of maths is very sequential, but to successfully complete many maths problems a very strict sequence must be followed. Learning times tables is all about learning a strict sequence of information.
- Orientation. Difficulties with orientation and direction can lead to confusion of maths symbols. Some people with dyslexia show weakness in the Coding subtest in the assessment meaning that they struggle to decode symbols accurately and quickly.
- Memory. There are many facts, figures, tables and formulas which have to be learnt and recalled accurately.
- Confidence. A lack of confidence in their own maths ability can exacerbate the above difficulties.
When dyscalculia is suspected, a detailed diagnostic evaluation should be performed. The primary task of specialists in child and adolescent psychiatry, and of the school health services, is to determine whether any comorbid (associated) disturbances are present. The differential evaluation of performance on numerical-arithmetical and non-numerical skills lies in the area of competence of school psychologists and neuropsychologists. Ideally, the performance profile that is generated by the diagnostic evaluation should serve as a point of departure for intervention planning.
Many children and adolescents with dyscalculia have associated cognitive dysfunction (e.g., impairment of working memory and visuospatial skills), and 20% to 60% of those affected have comorbid disorders such as dyslexia or attention deficit disorder (ADHD) 1.
Many affected children acquire a negative attitude to counting and arithmetic, which, in turn, often develops into a specific mathematics anxiety or even a generalized school phobia 4. Unless specifically treated, dyscalculia persists into adulthood 5; it can lastingly impair personality development, schooling, and occupational training. Dyscalculia is also an economic issue, as adults with poor arithmetic skills suffer a major disadvantage on the job market 6. About 22% of young adults fall into this category 7. The mental disorders commonly associated with dyscalculia are expensive to treat 8. Thus, the early recognition and differential diagnosis of learning disorders are an important matter not just for child psychiatrists, who must often deal with the secondary conditions that arise from these disorders, but also for general practitioners and pediatricians, as the delayed acquisition of pre-scholastic skills in the nursery and kindergarten years may already be an early sign of a problem 9.
The few interventional studies that have been published to date document the efficacy of pedagogic-therapeutic interventions directed toward specific problem areas. The treatment is tailored to the individual patient’s cognitive functional profile and severity of manifestations. Psychotherapy and/or medication are sometimes necessary as well.
In summary, the main role of the treating pediatrician or family physician centers on the early recognition of dyscalculia (and other learning disorders) and on counseling of the child’s parents and other carers about the further diagnostic and therapeutic measures that are indicated. Early recognition largely depends on information provided by the child’s parents or other carers. Depending on the age of the child, specific questions should be asked about his/her understanding of quantity, counting skills, and mathematical performance in school to date. The history should also include questions about any secondary disturbances that might be present, e.g., learning disorders in other areas and/or psychopathological manifestations, dislike of school, mathematics anxiety, and/or school phobia.
Dyscalculia symptoms
Mental illness is much more common among children with learning disorders than among age-matched children without learning disorders (30–50% versus 8–18%) 10. Children with dyscalculia often have severe emotional distress because they do poorly in school; this can lead, in turn, to a negative attitude about mathematical tasks or even to mathematics anxiety and school phobia 4. Mathematics anxiety tends to become chronic and to persistently impair skill development. Its effects can be seen on multiple levels—physiological (palpitations, diaphoresis), cognitive (feelings of helplessness, impaired working memory) 11 and behavioral (avoidance). Severe mathematics anxiety also seems to impair basic numerical processing: The mental representation of number is less precise in persons with severe mathematics anxiety than in persons with mild or no mathematics anxiety 12.
Even though the disorder is heterogeneous, certain aspects of numerical calculating skills do seem to be especially common in, and characteristic of, patients with dyscalculia.
Numerical-arithmetical skills that present particular difficulty to children with dyscalculia and mathematical learning disability 13:
- The acquisition, recall, and application of numerical-arithmetical knowledge, including numerospatial conceptualization and both factual and procedural arithmetical knowledge
- Wrong or inappropriate application of calculating strategies
- Difficulty generalizing learned content
- Little or no knowledge transfer, i.e., no automatic transfer of learned content to other tasks or problem areas without external help
Causes of dyscalculia
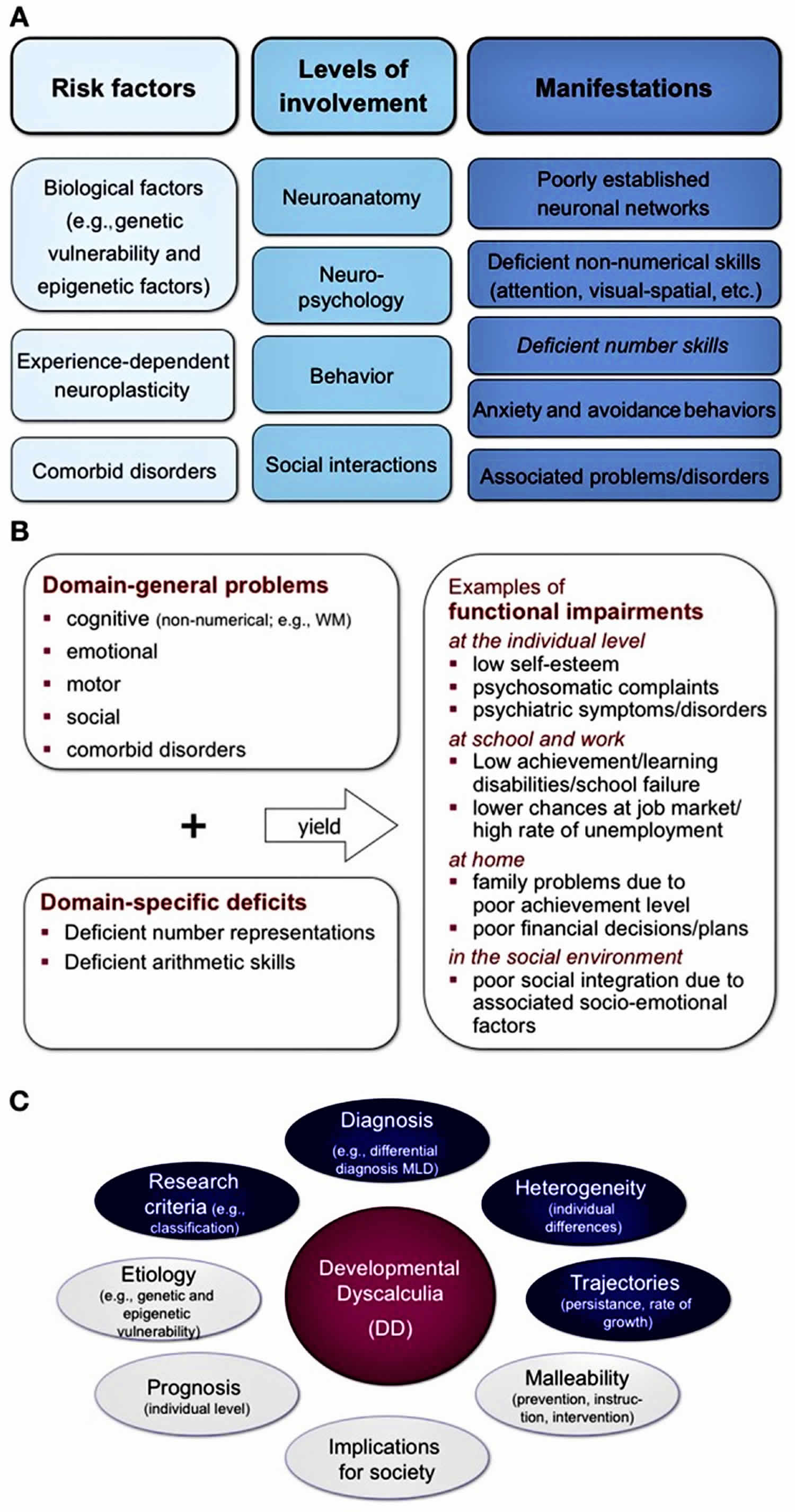
Dyscalculia has many contributory causes. Dyscalculia is not a single, uniform entity; rather, its subtypes can be classified systematically and in detail on the basis of their varying causes, underlying neural bases, cognitive representations, and skills levels (Figure 1). However, no firm conclusions can yet be drawn about the relations and interactions between them, as too little evidence is available. There is, however, a consensus in the current literature supporting the multifactorial origin of developmental dyscalculia and other learning disorders 3. Dyscalculia is also often present in children suffering from neurological diseases (e.g., epilepsy, premature birth, metabolic disorders) and genetic syndromes (e.g., fragile X syndrome, Williams-Beuren syndrome, velocardiofacial syndrome) 1.
Developmental dyscalculia tends to run in families 14, possibly because of a genetic predisposition 15.
There may be a primary genetic vulnerability to the impaired development of basic numerical functions or of linguistic, visuospatial, and executive ones. As we now know, the maturation of these functions can also be affected by environmentally determined, epigenetically mediated influences, such as stress (Figure 1). This explains the marked association of dyscalculia with attention deficit hyperactivity disorder (ADHD) on the one hand, and with dyslexia on the other.
Figure 1. Potential causative factors for dyscalculia
[Source 1 ]Figure 2. Development and integrative perspective on developmental dyscalculia
Comorbidities commonly associated with dyscalculia
According to von Aster and Shalev 3, 20% to 60% of all persons with dyscalculia also have learning difficulties of other types, e.g., dyslexia 17 or ADHD 18. A combination of dyslexia and dyscalculia was found in 7.6% of 788 randomly sampled Dutch fourth- and fifth-graders 19. Even among ninth-graders, 52% of the variance in calculating ability was accounted for by reading skills 20. It even seems to be the case that deficient phonological skills (considered the most important precursor skill for written language) in preschool children are associated with poorer performance on formal calculating tasks in the early years of primary school 21. A disorder of linguistic development in nursery-school and kindergarten age seems to be a risk factor for poor calculating ability 22.
Only scant empirical data are available to date on the comorbidity of dyscalculia with attention deficit disorders (ADHD). Rubinsten and colleagues 23 studied the effects of methylphenidate, a stimulant, on calculating ability in three groups of children with ADHD: The first group had no learning disorder, the second had a mathematical disability, and the third had dyscalculia. In all groups, the stimulant was found to improve those aspects of calculating ability that depend on working memory (e.g., “carrying” while calculating with multi-digit numbers), but it had no effect on basic numerical skills. The authors concluded that children who have both ADHD and either mathematical disability or dyscalculia need not only pharmacotherapy, but also specific learning therapy.
Dyscalculia diagnosis
Physicians’ first responsibility when consulted for dyscalculia is to consider whether there is any evidence for a biologically treatable neurological disorder such as epilepsy or a genetic, metabolic, or structural brain disorder that might mandate EEG, brain imaging, or other investigations 24. Physicians concerned with development need to discuss with the parents how far to go in probing for the biologic cause of dyscalculia, making clear which tests are for the child’s or family’s benefit and which to answer research questions. Physicians more pressing responsibility is to probe for the highly prevalent associated developmental problems such as attention-deficit disorder (ADHD), anxiety, or depression amenable to counseling and pharmacologic interventions, and for unfavorable environmental circumstances to be addressed. Dealing with these nonspecific issues together with cognitive counseling may determine the success or failure of remedial educational interventions.
Practical experience shows that there is a wide variety of performance profiles for numerical and calculating skills; this fact suggests that there are different subtypes of dyscalculia 25. When dyscalculia is suspected, a detailed diagnostic evaluation is needed in order to take proper account of the complexity of this learning disorder and to produce an accurate picture of the affected child’s particular strengths and weaknesses in the area of numbers and calculations. The diagnostic instruments used for this purpose are of two main types, the curricular and the neuropsychological (see Table 1). As the affected children often perform far below grade level on numerical and calculating tasks, the use of curricular tests alone may not yield a complete picture of the actual performance deficit; this can, in turn, lead to inappropriate interventions with little promise of efficacy, because the child’s performance is not really at the level for which the intervention was designed.
Specific questions for history-taking in suspected dyscalculia
These questions are a small component of the overall assessment of the child’s health and mental and physical developmental state.
- Cause
- Family history — Are/were there any other family members (e.g., mother, father, siblings) who had difficulty learning to perform arithmetic?
- Primary vs. secondary — Did the child have difficulty learning to perform arithmetic, or a particular aversion to arithmetic, from the very beginning, or did the problem only begin later, e.g., in the aftermath of an illness or other serious life event (including neurological and psychiatric disease and traumatic brain injury)
- Isolated dyscalculia vs. general learning impairment
- Does the child or adolescent attend a normal school?
- Does the child or adolescent have difficulty in other school subjects aside from mathematics? Are these difficulties so severe and/or present in so many subjects that the normal progression into the next grade might not be possible?
- Precursor skills
- Was the child or adolescent happy to deal with quantities and numbers as a preschool child? For example, did he or she perform normally with respect to number-rhymes, counting out loud, dividing groups of objects (e.g., sharing candies with friends), and playing board games?
- Could the child count to ten before starting school?
- Could the child recognize small numbers of objects (one, two, or three objects) at a glance before starting school?
- Appropriate fostering and schooling
- Did the child have adequate opportunity in the preschool and kindergarten years to incorporate quantitative concepts into play (e.g., to play board games)?
- Is there any reason to think that the child’s instruction in mathematics was, or is, deficient? For example, do many other children in the same class also have difficulty calculating?
- Associated problems
- Language development: Was language development delayed? (If so, then one should also expect difficulty with counting and other mainly linguistically based aspects of arithmetic, such as the recall of arithmetical facts [e.g., 2 × 3 = 6] or the performance of textual exercises)
- Visuospatial skills: Does the child or adolescent have difficulty drawing or copying geometrical figures (note: difficulties of this type can be hard to distinguish from impaired motor function while drawing) or difficulty with spatial and temporal orientation?
- Attention and working memory: Does the child or adolescent have difficulty in everyday life when confronted with more than one task at once? Does he or she often forget appointments, homework, etc.?
- Other learning disorders: Does the child or adolescent have, in addition to dyscalculia, difficulty acquiring written language (reading, spelling)?
- Accompanying social and emotional problems: Does the child seem to suffer from mathematics anxiety, dislike of school, or school phobia?
- Psychosomatic complaints: Does the child or adolescent ever complain of headache, abdominal pain, etc., when a mathematics test is scheduled or mathematics homework is due?
- Current school performance in mathematics: What grade did the child most recently get in mathematics?
- What aspects of arithmetic does the child or adolescent currently do well, and what aspects or components present special difficulty? (Note: Here, one should ask not only about the elementary operations [which can be affected independently to differing degrees], but also about algebra, geometry, etc.)
- Interventions and treatments to date
- What, if anything, has been done till now to improve the child or adolescent’s mathematical ability?
- Has any treatment been provided for other learning difficulties or behavioral problems?
- If so, what, and was it successful?
Dyscalculia test
There are some standardized tests of various calculation skills, but none that is universally accepted 24.
Table 1. Comparison of two types of test for numerical-arithmetical skills
| Curricular tests(school performance tests) | Neuropsychologically oriented tests | |
| Concept | The test is oriented toward the mathematics curriculum in the child’s grade. Its main purpose is to determine whether the child has met the learning objectives for his or her grade. | The test is designed to assess basic numerical and arithmetical skills and to take account of non-numerical functions. |
| Its main purpose is to generate a performance profile for numerical-arithmetical skills and to determine the cause of difficulty calculating (i.e., to identify the underlying learning processes and mechanisms). | ||
| Manner of testing | Usually designed as power tests (i.e., only the correct answer is relevant); they are also usable as group or class tests (economy of use) | Attention is paid not only to correct answers, but also (at least for relevant components of the test) to processing speed and solving strategies, with the goal of a qualitative assessment of performance; thus, these tests can only be performed on an individual basis. |
| Diagnostic criterion (in many, but not all tests in the category in question) | percentile rank <10 | percentile rank <10 |
| some tests not only include a strict cut off at percentile rank <10 but also state the area in which additional help is likely to be needed (e.g., percentile rank 10<25 in tedi-math) | ||
| combined with average intellectual peformance (according to ICD-10); | ||
| Examples | ERT for grades 1–4 (e.g., ERT 1+; ERT 2+; ERT 3+; ERT 4+; | RZD 2–6 for grades 2–6; |
| TEDI-MATH for pre-kindergarten to grade 3; | ||
| DEMAT for grades 1–4: DEMAT 1; DEMAT 2; DEMAT 3; DEMAT 4 | ZAREKI-R for grades 1–4; | |
| ZAREKI-K for preschool children |
Abbreviations: DEMAT = Deutsche Mathematiktests; ERT = Eggenberger Rechentest; RZD = Rechenfertigkeiten- und Zahlenverarbeitungs-Diagnostikum; TEDI-MATH= Test zur Erfassung numerisch-rechnerischer Fertigkeiten; ZAREKI-R = die neuropsychologische Testbatterie für Zahlenverarbeitung und Rechnen bei Kindern, revidierte Version; ZAREKI-K = die neuropsychologische Testbatterie für Zahlenverarbeitung und Rechnen bei Kindern, Kindergarten Version. All of these tests except ZAREKI are published by Hogrefe (www.testzentrale.de). The ZAREKI-R and the ZAREKI-K for 4-and 5-year-olds are available from Pearson Assessment (www.pearsonassessment.de)
[Source 1 ]In children of kindergarten age, specific precursor skills can be identified (Table 2) that have been found to be reliable predictors of later calculating ability 26. Working memory has also been found to be such a predictor 27. Most standardized tests of calculating ability are designed for primary-school children and are not normed for any higher level than the sixth grade 28. The BASIS-MATH 4–8 test, which was published in 2010, is the only German-language test that can be used up to the eighth grade 29. It provides no normed data, but rather a single threshold value for the fourth through eighth grades, which can be interpreted as a rough indication of the mastery of basic mathematical concepts. BASIS-MATH has proved its usefulness in practice, as it yields not just a quantitative test score, but also information about the child’s calculating strategies, which can be of service in the planning of therapeutic interventions.
Table 2. Age specific numerical-arithmetical functions and relevant skills in each functional area
| Numerical-arithmetical functional areas (age/grade) | Skills and tasks |
| Basic numerical skills and precursor skills (preschool, nursery school, kindergarten) | Understanding of quantity (e.g., tasks requiring a comparison of quantities and numbers), rapid recognition of small quantities, mastery of counting skills, identification of Arabic numerals |
| Arithmetical factual knowledge (primary school) | Single-digit addition and multiplication, e.g., 3+2 or 3×2 |
| Arithmetical procedures(from primary school onward) | Knowing the correct sequence of solution steps for multistep calculating tasks |
| Arithmetical reasoning; conceptual arithmetical knowledge (from primary school onward, highly dependent on teaching methods) | Knowledge of the involved quantities and partial quantities, knowledge of the similarities and differences between different tyes of operations, comprehension of arithmetical procedures |
Dyscalculia treatment
The treatment of children and adolescents with dyscalculia is a complex matter because of the heterogeneity of the disorder and the comorbid disorders often associated with it. For the best chance of a lasting therapeutic benefit, the treatment should be individually tailored to the findings of the diagnostic evaluation. It should be adapted to the patient’s individual cognitive functional profile and may incorporate medications and psychotherapy as well, if these are warranted by severe accompanying psychopathological manifestations such as anxiety, depression, or ADHD 30.
The following skills are particularly important for the domain-specific aspects of treatment:
- basic numerical skills,
- the establishment and consolidation of numero-spatial representations,
- the development of arithmetical reasoning,
- procedural knowledge, and
- the automatization of factual knowledge.
All of these skills fundamentally depend on successively acquired layers of understanding, in constant interaction with the practicing of skills for their consolidation. For example, when a child acquires arithmetical facts, attention should be paid to the basic underlying arithmetical reasoning, as well as to frequent practice. As can be seen from the examples in Table 3, the various solving strategies differ both with respect to the complexity of the solution procedures involved and with respect to the underlying arithmetical reasoning. Counting up from the first sum to the answer is an immature solving strategy compared to breaking down the problem into its several components, but it is, at least, more mature and reflects a better comprehension of arithmetic than simply counting everything that is to be summed. The latter immature strategy demands more from working memory, which must store both interim results, 6 and 4. Repeated practice fosters the automatic recall of learned content, thereby lessening the demand on working memory. This demand is especially high in multi-digit calculations with carrying, where interim results must be retained and manipulated (e.g., adding 87 and 45).
Table 3. Illustration of various solution pathways and strategies for single-digit addition and multiplication tasks (also called “arithmetical facts”)
| Solution strategy | Task: | |
| 6 + 4 | 7 × 2 | |
| Direct recall | 6 + 4 = 10 | 7 × 2 = 14 |
| Count everything | 1 + 1 + 1 + 1 + 1 + 1 = 6; 1 + 1 + 1 + 1 = 4; 6 + 4 = 10 | − |
| Count from first sum up | 6 + 1 = 7, 7 + 1 = 8, 8 + 1 = 9, 9 + 1 = 10 | − |
| Breaking the problem down into components (focus on base 5) | 5 + 4 = 9 9 + 1 = 10 | (5 × 2) + (2 × 2) |
| Breaking the problem down (base 5) with movements | (6 − 1) + (4 + 1) =5 + 5 = 10 | − |
| Repeated addition | – | 2 + 2 + 2 + 2 + 2 + 2 + 2 |
| Other strategies | 6 + 6 = 12 12 − 2 = 10 | (10 × 2) – (3 × 2) |
Most of the empirical studies on interventions to improve calculating ability have been carried out in English-speaking countries by special-education professionals. Their findings are, to some extent, inconsistent. A meta-analysis by Kroesbergen and van Luit 13 of 58 interventional studies among primary-school pupils revealed that:
- most interventions dealt with basic numerical skills;
- interventions to promote basic numerical skills were more effective than interventions to promote precursor skills and/or problem-solving strategies; the sample size varied from 3 to 376, and the Cohen’s d values (effect sizes) from –0.44 to above 3 13;
- shorter interventions were more effective than longer ones (the duration of interventions ranged from one week to one year across studies);
- interventions performed in person by teaching staff (“direct instruction”) were more effective than computerized ones (“mediated instruction”).
A further meta-analysis of studies of individualized intervention in the English-speaking countries revealed that individualized intervention is highly effective at improving calculating ability 31, that the particular method of intervention that is used largely determines the degree of effectiveness, and that interventions conveying an understanding of strategy are much more effective than those in which the subject matter is passively communicated (“strategy instruction” versus “direct instruction”).
The following methods of intervention were found to be especially effective:
- repeated practice;
- segmentation of subject matter;
- small, interactive groups;
- the use of cues in strategy-learning 31.
A recently published meta-analysis by Ise and colleagues 32 evaluated eight studies from the German-speaking countries. The overall effect strength was 0.50, which is considered an intermediate value (neither strong nor weak). No difference in effectiveness was found between curricular and non-curricular treatment approaches, but all interventions tended to be more effective the longer and the more intensively they were carried out. Most of the currently available German-language programs for promoting numerical calculating skills have not been empirically tested for efficacy, and many seem to lack an adequate theoretical basis.
The scientifically studied learning programs in the German-speaking countries include “Mengen, Zählen, Zahlen” (MZZ; “Quantities, Counting, and Numbers”), which was designed for preschool children 33; the computerized and largely curricular intervention programs “Elfe und Mathis” (“Elfe and Mathis”) 34; and the learning program “Calcularis” 35, which is based on neuroscientific models of the development of number processing and arithmetic. The effect strength of these intervention programs has not been studied. MZZ is intended to promote the establishment of basic numerical and scholastic precursor skills (the concepts of quantity and number, counting order, and various types of notation). “Calcularis” begins with basic numerical skills and addresses the automatization of various number representations in increasingly large numerical domains, the understanding of arithmetical operations, and the establishment of factual arithmetical knowledge. “Calcularis” has an adaptive structure, i.e., it can be adapted to the individual child’s learning difficulties. In a study of a “Calcularis” prototype with functional neuroimaging (fMRI), the improvement in numerical-spatial and arithmetical skills was found to be associated with altered patterns of neural activation in the frontal and parietal lobes 36.
- Kaufmann L, von Aster M. The diagnosis and management of dyscalculia. Dtsch Arztebl Int. 2012;109(45):767-77; quiz 778. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3514770/[↩][↩][↩][↩][↩][↩][↩][↩]
- Dyscalculia and the Calculating Brain. Pediatr Neurol. 2016 Aug;61:11-20. doi: 10.1016/j.pediatrneurol.2016.02.007. Epub 2016 Feb 18. https://www.ncbi.nlm.nih.gov/pubmed/27515455[↩]
- von Aster MG, Shalev R. Number development and developmental dyscalculia. Dev Med Child Neurol. 2007;49:868–873.[↩][↩][↩]
- Krinzinger H, Kaufmann L. Rechenangst und Rechenleistung. Sprache, Stimme, Gehör. 2006;30:160–164.[↩][↩]
- Gerber PJ. The impact of learning disabilities on adulthood: a review of the evidenced-based literature for research and practice in adult education. J Learn Dis. 2012;45:31–46.[↩]
- Kaufmann L, Pixner S, Goebel S. Finger usage and arithmetics in adults with math difficulties: Evidence from a case report. Front Psychol. 2011;2[↩]
- NRDC/National Research and Development Centre for Adult Literacy and Numeracy (2008) London: NRDC; Research Briefing Numeracy.[↩]
- Butterworth B, Varma S, Laurillard D. Dyscalculia: From brain to education. Science. 2011;332:1049–1053.[↩]
- von Aster M,G, Schweiter M, Weinhold-Zulauf M. Rechenstörungen bei Kindern: Vorläufer, Prävalenzen und psychische Störungen. Zeitschrift Entwicklungspsychol Pädagog Psychol. 2007;39:85–96.[↩]
- The mental health needs of children and adolescents with learning disabilities. Vedi K, Bernard S. Curr Opin Psychiatry. 2012 Sep; 25(5):353-8.[↩]
- Mathematics anxiety and working memory: support for the existence of a deficient inhibition mechanism. Hopko DR, Ashcraft MH, Gute J, Ruggiero KJ, Lewis C. J Anxiety Disord. 1998 Jul-Aug; 12(4):343-55.[↩]
- The effect of mathematics anxiety on the processing of numerical magnitude. Maloney EA, Ansari D, Fugelsang JA. Q J Exp Psychol (Hove). 2011 Jan; 64(1):10-6.[↩]
- Kroesbergen E, van Luit JEH. Mathematics Intervention for Children with Special Educational Needs. Remedial and Special Education. 2003;24:97–114.[↩][↩][↩]
- Developmental dyscalculia is a familial learning disability. Shalev RS, Manor O, Kerem B, Ayali M, Badichi N, Friedlander Y, Gross-Tsur V. J Learn Disabil. 2001 Jan-Feb; 34(1):59-65.[↩]
- Learning Abilities and Disabilities: Generalist Genes, Specialist Environments. Kovas Y, Plomin R. Curr Dir Psychol Sci. 2007 Oct; 16(5):284-288.[↩]
- Kaufmann L, Mazzocco MM, Dowker A, et al. Dyscalculia from a developmental and differential perspective. Front Psychol. 2013;4:516. Published 2013 Aug 21. doi:10.3389/fpsyg.2013.00516 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3748433/[↩]
- Landerl K, Moll K. Comorbidity of learning disorders: Prevalence and familial transmission. J Child Psychol Psychiatry. 2010;51:287–294.[↩]
- Rubinsten O. Co-occurence of developmental disorders: The case of developmental dyscalculia. Cognitive Development. 2009;24:362–370.[↩]
- Dirks E, Spyer G, van Lieshout EC, de Sonneville L. Prevalence of combined reading and arithmetic disabilities. J Learn Disabil. 2008;41:460–471[↩]
- Korhonen JG, Linnanmäki K, Aunio P. Language and mathematical performance: a comparison of lower secondary school students with different levels of mathematical skills. Scand J Educ Res. 2011[↩]
- Jordan JA, Wylie J, Mulhern G. Phonological awareness and mathematical difficulty: a longitudinal perspective. Br J Dev Psychol. 2010;28:89–107[↩]
- Manor O, Shalev RS, Joseph A, Gross-Tsur V. Arithmetic skills in kindergarten children with developmental language disorders. Eur J Paediatr Neurol. 2001;5:71–77[↩]
- Rubinsten O, Bedard AC, Tannock R. Methylphenidate improves general but not core numerical abilities in ADHD children with co-morbid dyscalculia or mathematical difficulties. J Open Psychol. 2008;1:11–17.[↩]
- Dyscalculia and the Calculating Brain. Pediatric Neurology , Volume 61 , 11 – 20 https://www.pedneur.com/article/S0887-8994(16)00067-9/fulltext[↩][↩]
- Wilson AJ, Dehaene S. Number sense and developmental dyscalculia: Human behavior, learning, and the developing brain. In: Coch D, Dawson G, Fischer K, editors. Atypical development. New York: Guilford Press; 2007. pp. 212–238.[↩]
- Aunio P, Niemivirta M. Predicting children’s mathematical performance in grade one by early numeracy. J Lean Indiv Diff. 2010;20:427–435.[↩]
- Toll SW, Van der Ven SH, Kroesbergen EH, Van Luit JE. Executive functions as predictors of math learning disabilities. J Learn Disabil. 2011;44:521–532.[↩]
- Jacobs C, Petermann F. Göttingen: Hogrefe; 2005. Rechenfertigkeiten- und Zahlenverarbeitungs-Diagnostikum für die 2 Bis 6. Klassen.[↩]
- Moser Opitz E, Reusser L, Moeri Müller M, Anliker B, Wittich C, Weesemann O, Ramseier E. Göttingen: Hogrefe; 2010. BASIS-MATH 4-8. Basisdiagnostik Mathematik für die Klassen 4-8.[↩]
- Galonska S, Kaufmann L. Intervention bei entwicklungsbedingter Dyskalkulie. Sprache Stimme Gehör. 2006;30:171–178.[↩]
- A meta-analysis of single-subject-design intervention research for students with LD. Swanson HL, Sachse-Lee C. J Learn Disabil. 2000 Mar-Apr; 33(2):114-36.[↩][↩]
- Ise E, Dolle K, Pixner S, Schulte-Körne G. Effektive Förderung rechenschwacher Kinder: Eine Metaanalyse. Kindheit und Entwicklung. 2012;21:181–192.[↩]
- Krajewski K, Nieding G, Schneider W. Die Welt der Mathematik entdecken. Berlin: Cornelsen; 2007. „Mengen, zählen, Zahlen“[↩]
- Lenhard A, Lenhard W, Klauer KJ. Förderung des logischen Denkvermögens für das Vor- und Grundschulalter. Göttingen: Hogrefe; 2011. Denkspiele mit Elfe und Mathis. [↩]
- Von Aster MG, Käser T, Kucian K, Gross M. Calcularis – Rechenschwäche mit dem Computer begegnen. Schweizerische Zeitschrift für Heilpädagogik. 2012;18:32–36[↩]
- Mental number line training in children with developmental dyscalculia. Kucian K, Grond U, Rotzer S, Henzi B, Schönmann C, Plangger F, Gälli M, Martin E, von Aster M. Neuroimage. 2011 Aug 1; 57(3):782-95.[↩]